The figure of the Yagi antenna at the left shows the elements unsupported in free space. This is an excellent way to start analyzing a pure Yagi array. However it may eventually be desired to include the effects of a conductive support boom.
All thin wire computer codes used for radiation and scattering problems (antenna and radar) problems make simplifying assumptions to make the problem tractable. Without these assumptions the program would not be practical to use for general problems. The program ASAP, discussed on these pages, and even NEC (Numerical Electromatic Code -- available elsewhere on the internet) are no exception.
What is the Thin Wire Assumption?
The "Thin Wire" assumption, simply put, is that the current exists only at the surface of the wire and only has components along the axis of the wire. There is no current, and therefore no conductivity, across the wire or around the circumference. The axial directed current is allowed to change its value with distance along the wire but this surface current is uniform all the way around the wire at a given point.
It should be noted, that the thin wire assumption does not ignore the thickness of the wire. Indeed it is absolutely essential to consider the thickness when computing the interaction of the axial surface current with the electromagnetic field. The thin wire assumption just ignores the component of current across the wire. Normally this causes no problems and the answer obtained is negligibly difference from the "real" answer. However there are many types of practical problems where some of the antenna parameters may be affected by this assumption.
An Example Antenna That Could Use Some Thick Wires
There are several occasions when ignoring the current across the wire will not be insignificant in the real-world. One example of this would be an attempt to represent a support boom for a Yagi antenna using a single wire in the analysis model.
|
|
The figure of the Yagi antenna at the left shows the elements unsupported in free space. This is an excellent way to start analyzing a pure Yagi array. However it may eventually be desired to include the effects of a conductive support boom. |
|
The figure of the Yagi antenna at the right shows the elements "supported" by a conductive rod. This is like many real Yagi antennas. However attempts at modeling the support boom/rod as a single wire in a thin wire computer code is doomed to failure. |
|
The computer model wire has no conductivity at all across the wire so the model wire does not respond to the strong near fields. In real life, the support boom "shorts out" (so to speak) the E-field of the antenna elements resulting in changes to the stored energy in the near field. The process of "shorting out" the near field of the antenna element would lead to a small current flowing crosswise to the axis of the support boom. The width of the boom and the currents on it are insignificant from the point of view of the radiation pattern of the antenna but the change to the near field stored energy produces a shift in the resonant frequency of each element. This can be quite significant in many practical antennas. The computer code's thin wire assumption does not support the crosswise current component and therefore does not "short out" the near field. Therefore, attempts to model this support boom with a single wire will not succeed. A possible method using multiple wire segments will be discussed later on in this page. First, however, the thin wire assumption will be discussed more completely.
A Closer Look at the Thin Wire Assumption
Below is an diagram showing a long wire that has been broken into segments for modeling. One of these segments is enlarged to illustrate the concept of how the currents are modeled in thin wire programs such as ASAP. The same concept also applies to other thin wire programs such as NEC. It should be noted that breaking the wire into segments is not the essence of the thin wire assumption (or the moment method for that matter) but is convenient for illustration purposes since that is the way most thin wire programs work.
The first assumption is the that the currents exist only on the surface of the wire. This is a realistic assumption as long as the wire is a sufficiently good conductor and the frequency is sufficiently high. Under normal circumstances these conditions are easily satisfied. Even at very low frequencies (such as 60 Hz) other limitations of the computer algorithm are likely to introduce more error than this assumption.
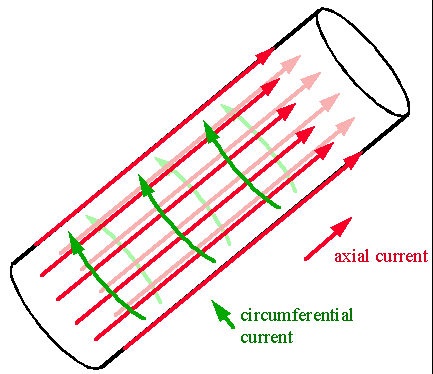On a real wire segment, the surface currents will have both axial and circumferential components. These currents are illustrated in the diagram with the red arrows representing the surface current in the axial direction and the green arrows representing the circumferential current.
The primary assumption that the thin wire code makes is that all of the surface current on the wire is in the direction of the axis and that there is no current around the wire. This means that only the current shown by the red arrows is computed for interactions with the electromagnetic field. The currents shown in green are assumed not to exist. This assumption normally does not cause problems. This is because one of the input conditions to the program is that the wire radius must be a very small fraction of a wavelength. Since the wire diameter is so small compared to a wavelength, any currents that might exist around the wire are normally insignificant. There are, however some wire geometries where cross components can become important. This will be discussed in another section.
Despite the wire radius being small compared to a wavelength, there is an effect that must be considered. All general purpose thin wire codes (including ASAP and NEC) do, indeed must, consider the finite radius of the wire when computing the interaction of the surface current with the electromagnetic field. Without taking into account wire radius, realistic answers would not be possible for antenna impedance (among other things).
Even though wire radius is considered for the interaction of electromagnectic fields with the wire, the field produced by the wire segment is generally assumed to come from an equivalent current element located on the axis of the wire. This situation is only physically equivalent if the original surface current is distributed uniformally all the way around the wire. The computer code is designed with the assumption that the surface current is always uniform so that the axial current element can be used.
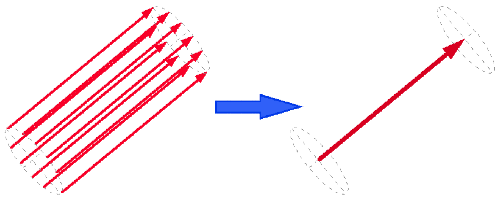
There are physical cases where this assumption is not justified. In the example below two parallel segments taken from a parallel line transmission line is shown. In "real life" the current will tend to crowd toward the inside surfaces of the wire. This makes the effective spacing of the wires closer together than what the axial model of current would predict. This effect is small as long as the wire radius is very small compared to the separation distance. In the case shown where the distance is comparable to the wire radius, the effect could be appreciable.
A possible method of dealing with this situation is to model with real wires with a network of smaller model wires that are connected to each other. This will be considered on the next page.
A method to model real wires with a network of smaller model wires on the next page.
Or
Go back to the Main Examples Page
Including:
See also the quick reference for the user's guide.
Goto Systems Manual
(Theory of Operation)
Return to ASAP Homepage
Last modified on: 3 Nov 2007
